Fonctions logiques et tables de vérité

Définir les fonctions logiques et les tables de vérités qui leurs sont associées est le point de départ pour parler des portes logiques.

De nombreux sites traitent ce sujet, dont wikipedia, mais je souhaite également reprendre ces informations afin d'être le plus exhaustif possible. Ainsi, si tu découvres ce sujet via mon site (ce dont je doute fort...), tu auras toutes les infos.

Comme je l'ai déjà dit dans un autre article, je n'ai pas vraiment de formation en électronique, ainsi, je peux m’éloigner un peu du formalisme conventionnel, tu m'en excuseras !

Je garde les noms des fonctions logiques anglaises, par habitude et par praticité car j'utilise volontiers les diminutifs pour designer les fonctions et ces diminutifs proviennent du nom anglais.

Le principe des fonctions logiques est de donné un résultat de sortie "OUT" en fonction des entrées "IN" aussi désignées "A" et "B". On peut faire une première classification fonction du nombre d'entrées que possède la fonction : 1 ou 2. Il est possible de créer des fonction à plus de 2 entrées mais je m’arrête à 2.

Les valeurs que peuvent avoir les entrées et les sorties sont binaires : 0 ou 1. On peut aussi parler de VRAI ou FAUX, mais je parlerai de 0 ou 1.

Fonctions logiques à une entrée

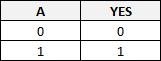
Fonction logique YES (OUI)

L'état de la sortie est le même que l'état de l'entrée.

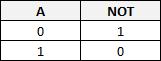
Fonction logique NOT (NON)

L'état de la sortie est l'inverse de l'état de l'entrée.

Fonctions logiques à deux entrées

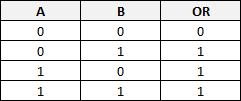
Fonction logique OR (OU)

L'état de la sortie vaut 1 si au moins une des entrées vaut 1.

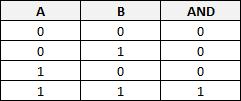
Fonction logique AND (ET)

L'état de sortie vaut 1 seulement si les deux entrées valent 1.

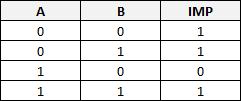
Fonction logique IMP (IMPLICATION)

Cette fonction n'a pas de diminutif explicite, alors je lui attribue celui là...

L'état de sortie vaut 1 si A vaut 0 (peu importe l'état de B) ou si A vaut 1 et B vaut 1.

Fonction logique NOR (NON OU)

C'est l'inverse de la fonction OR.

L'état de sortie vaut 1 seulement si les entrées valent 0.

Fonction logique NAND (NON ET)

C'est l'inverse de la fonction AND.

L'état de sortie vaut 1 sauf si les deux entrées valent 1.

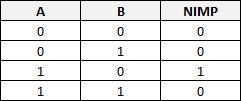
Fonction logique NIMP (NON IMPLICATION)

C'est l'inverse de la fonction IMP.

L'état de sortie vaut 1 si A vaut 1 et B vaut 0.

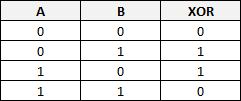
Fonction logique XOR (OU EXCLUSIF)

L'état de sortie vaut 1 si les états des entrées sont différentes.

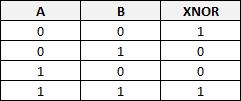
Fonction logique XNOR (NON OU EXCLUSIF)

C'est l'inverse de la fonction XOR.

L'état de sortie vaut 1 si les états des entrées sont identiques.